Laurance R. Doyle1, Hans-Jörg Deeg2,3, Valerij P. Kozhevnikov4, Brian Oetiker5, Eduardo L. Martín2, J. Ellen Blue6, Lee Rottler7, Remington P.S. Stone8, Zoran Ninkov9, Jon M. Jenkins10, Jean Schneider11, Edward W. Dunham12, Moira F. Doyle13, Efthimious Paleologou14
1SETI Institute, 2035 Landings Drive, Mountain View, CA 94043 (ldoyle@seti.org)
2Instituto de Astrofísica de Canarias, E-38200 La Laguna (Tenerife), Spain
(hdeeg@ll.iac.es)
3Centro de Astrobiología, E-28807 Torrejon de Ardoz (Madrid), Spain
4Astronomical Observatory, Ural State University, Lenin Ave. 51,
620083 Ekaterinburg, Russia
5University of New Mexico, Department of Astronomy and Physics,
Albuquerque, NM 87131
6SRI International, 333 Ravenswood Ave., Menlo Park, CA 94025
7University of California, Lick Observatory, 1156 High, Santa Cruz, CA 95060
8University of California, Lick Observatory, Mount Hamilton, CA 95040
9Center for Imaging Science, Rochester Institute of Technology, Rochester, NY 14623
10SETI Institute, MS 245-3, NASA Ames Research Center, Moffett Field, CA 94035
11CNRS-Observatoire de Paris, 92195 Meudon, France
12Lowell Observatory, Mars Road, Flagstaff, AZ 87000
13FIDM, 1212 Raintree Circle, Culver City, CA 90230
14University of Crete, Skinakas Observatory, P.O. Box 1527, 71110 Heraklion, Greece
Submitted to: The Astrophysical Journal
Received: August 18, 1999
Accepted: Dec. 1999
For reprints contact L.R. Doyle or
H.J. Deeg
Abstract
A lightcurve of the eclipsing binary CM Draconis has been analyzed for the presence of transits of planets of size >= 2.5 Earth-radii (Re), with periods of 60 days or less, and in co-planar orbits around the binary system. About 400 million model lightcurves, representing transits from planets with periods ranging from 7 to 60 days, have been matched/correlated against these data. This process we call the "transit detection algorithm" or TDA. The resulting `transit-statistics' for each planet candidate allow the quantification of detection probabilities, and of false alarm rates.
Our current lightcurve of CM Dra has a coverage of 1014 hours with 26,043 individual points, at a photometric precision between 0.2% and 0.7%. Planets significantly larger then 3Re would constitute a `supra-noise' detection, and for periods of 60 days or less, they would have been detected with a probability of 90%. `Subnoise' detections of smaller planets are more constrained. For example, 2.5 Re planets with 10-day periods or less would have been detected with an 80% probability. The necessity for predicted observations is illustrated with the nine top planet candidates that emerged from our TDA analysis. They are the planet candidates with the highest transit-statistics from the 1994-1998 observing seasons and, for them, transits for the 1999 observing season were predicted. Of the seven candidates that were then observationally tested in 1999, all were ruled out except one, which needs further observational confirmation. We conclude that the photometric transit method is a viable way to search for relatively small, inner extrasolar planets with moderate-sized telescopes using CCD photometry with a matching-filter analysis.
Subject Headings: Extrasolar
Planets - Stars: Eclipsing Binaries, Individual (CM Draconis), Planetary
Systems - Methods: Statistical - Techniques: Photometric
1. Introduction
The idea that extrasolar planets may be detected by transits across the disc of stars goes back to a suggestion by Struve (1951) with subsequent full development by Rosenblatt (1971) and Borucki and Summers (1984); (see also Hale and Doyle, 1994). Schneider and Chevreton (1990) first suggested that eclipsing binaries would be good candidates for such a search, based on their orbital planes already being nearly edge-on. There are a number of advantages to choosing small eclipsing binaries for such searches. These include the obvious advantage that eclipsing binary systems are already known to have their orbital planes very nearly edge-on to the observer's line-of-sight, with subsequent planet formation expected to take place near the same plane. An additional damping of planetary orbits into the binary plane due to precession could also add to their coplanarity (Schneider 1994; Schneider and Doyle 1995).
For detection of terrestrial-sized planets, smaller stellar systems are preferred as they exhibit greater brightness variations during the transit of a given sized planet. The stellar components of the CM Dra binary (A and B) have a total disc area of about 12% that of the solar disc, allowing an order-of-magnitude improvement in detectability. The luminosity of the two components is only 1.03% the solar luminosity, they have a separation of 3.76 solar radii (about 14.9 times the radius of CM Dra A; Lacy 1977), and a mutual orbital period of 1.268?389?861 days (Deeg et. al. 1998). Consequently, the nearest stable third body would have a period of somewhat less than 7 days (Holman and Wiegert 1999, and references therein), with planets of periods up to about 35 days receiving the same energy from CM Dra A&B as the terrestrial planets receive from the Sun.
As a photometric comparison, a Neptune-sized planet in transit across one of the components of the CM Dra system would cause a 0.8% drop in brightness, while an Earth-sized planet would cause an 0.07% decrease in the brightness. Ground-based 1-meter photometric precision may be limited to about 0.1% (Young et. al. 1991), but improvement up to 0.015% photometry with 4-meter-class telescopes- mainly from reduced atmospheric scintillation noise- can be expected (Gilliland and Brown 1992).
It should also be noted that planetary transit events will occur across the discs of close eclipsing binaries in a quasi-periodic manner, as the phase of the binary components will be different between subsequent planetary transits (see Fig.1 in Deeg et. al. 1998). Because these are quasi-periodic photometric attenuations they can provide unique signatures of transit events, ruling out attenuations due to starspots on the stellar limb, for example. Of most importance, such transit attenuations have a significantly shorter duration, on average, than single star transit events (50 minutes compared with several hours) and thereby show a sufficiently different power spectrum from major sources of observational variability, such as nightly extinction variations (Deeg et. al. 1998). However, detections do not take place in frequency space, as the power of occasional transits is minuscule compared to the total observational noise power. Thus the observed light curve needs to be "matched" (correlated) in the time regime against synthetic light curves of all possible transit models that could occur across the observational range of period-phase space (see Brandmeier and Doyle 1996, Jenkins et al. 1996, Deeg et. al. 1998).
As an aside, a further advantage of small eclipsing binaries as targets for photometric planet searches is that outer jovian-mass planets around such systems may also be detected without transits-using the same photometric data-by a precise timing of eclipse minima. As is well known, the mutual binary eclipse minima constitute a periodic signal in themselves whose periodic variations in time can be indicative of drifts in the position of the binary system toward or away from the observer due to a third mass in orbit around the binary system. The subsequent light travel time difference across the binary/third-mass barycenter produces the periodic variation in the time of eclipses (see, for example, Hertz et. al. 1995, Doyle et al. 1998). An analysis constraining the presence of outer jovian-mass planets with periods shorter then about 6 years around the CM Dra system is published separately (Deeg et. al. 2000).
The remainder of this paper will outline the observational coverage of CM Dra obtained by the TEP (Transit of Extrasolar Planets) Network, focus on a detailed description of the transit detection algorithm (TDA)-with its application to the search for planets of sizes >~ 2.5 Re around CM Dra with periods from 7 to 60 days-and finally discuss the resultant planetary candidates and their observational dismissal or confirmation.
2. Observational Coverage of CM Dra
A detailed description of observations of CM Dra taken in the years 1994-1996, along with a list of the observatories, detectors, data reduction procedures and software is given in Deeg et. al. 1998 (herein referred to as TEP1). Previous accounts of the TEP network are also given by Schneider and Doyle (1995), Doyle et al. (1996) and Deeg et. al. (1997).
Our total high precision observations
of CM Dra taken from 1994 through 1998 are included in the analysis presented
here. Observations in 1999 were performed to confirm or rule out specific
predicted planetary transit candidates that resulted from the TDA general
analysis, and results of these observations will be presented in Section
6. In addition to the data presented in TEP1, 250 hours of high-precision
observational coverage were obtained in 1997, 106 hours in 1998, and 41
hours in 1999. These more recent observations were performed at the Crossley
(0.9m) telescope at Lick Observatory, at the IAC80 (0.8m) and OGS (1m)
telescopes of the Instituto de Astrofisica de Canarias, the Kourovka 0.7m
telescope of the Ural State University in Ekaterinburg, Russia, and at
the Capilla Peak 0.6m of the University of New Mexico. A summary of all
TEP observations of sufficient photometric precision is given in Table
1. The total lightcurve, to date, consists of 26,042 data points with a
photometric precision (standard deviation over the mean differential brightness
of CM Dra) between 0.2% and 0.7%, giving 1014 hours of total coverage of
CM Dra. However, only the 1994-1998 observations -24,874 data points covering
973 hours-were used in the TDA search for planetary candidates. The specific
aperture photometry software developed for this project is presented in
Deeg and Doyle (1999).
Table 1. TEP Network Observational Coverage of CM Draconis (hours)
| Observatory | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | Total |
| Crossley(0.9m) | 65 | 50 | 46 | 21 | 72 | 41 | 295 |
| IAC(0.8m) | 38 | 62 | 22 | 43 | 20 | -- | 185 |
| Kourovka(0.7m) | -- | -- | 68 | 87 | -- | -- | 155 |
| Capilla(0.6m)1 | -- | -- | 18 | 99 | -- | -- | 117 |
| OHP(1.2m) | 11 | 34 | 22 | -- | -- | -- | 67 |
| Mees(0.6m) | 53 | -- | -- | -- | -- | -- | 53 |
| INT(2.5m) | -- | -- | 42 | -- | -- | -- | 42 |
| JKT(1.0m) | -- | 39 | -- | -- | -- | -- | 39 |
| WISE(1.0m) | -- | -- | 28 | -- | -- | -- | 28 |
| Skinakas(1.3m) | 19 | -- | -- | -- | -- | -- | 19 |
| OGS(1.0m) | -- | -- | -- | -- | 14 | -- | 14 |
| Total | 186 | 185 | 246 | 250 | 106 | 41 | 1014 |
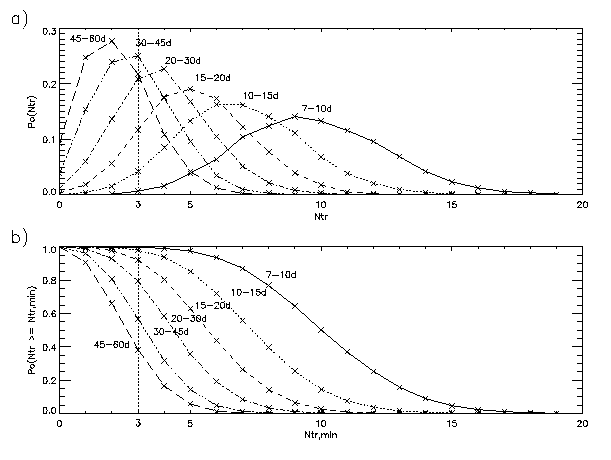
Within the 973-hour (1994-1998) light curve, many possible transit events could have occurred. This can be characterized by the number of transits, Ntr, that would have been observed, if a planet with a particular period would have been present. Ntr takes into account that a planet orbiting an eclipsing binary normally causes two transits events per period (see Fig. 1 in TEP1). The probabilities that a planet with random epoch and period (within certain period ranges) causes a specific number of transits in the observed lightcurve we will call the "observational probability" po(Ntr) (see Fig. 1a). In addition to being in the observational data, however, the transit events have to give a sufficiently strong signal (i.e. total sum of transit event depths compared to the background noise level) for a given candidate to be detectable. The probability of a given transit signal being detectable above the noise, which we will call the "intrinsic detection probability", pi, will be given in Section 4, following standard detection theory. The overall probability of detection of a given planetary transit candidate, pd, then is:
pd = po pi (1).
Since a single transit from a large planet (significantly larger then 3Re) would have been fairly obvious in the lightcurve (and therefore has pi = 1), its probability of detection is pd = po(Ntr,min = 1), where po(Ntr,min) is the probability that at least Ntr,min transits are in the lightcurve (Fig. 1b). For planets larger than 3Re then, from the data of Figure 1b, we have po ~ 90% for planetary periods of 60 days, with po being significantly greater for shorter periods, (po ~ 98% for periods of 25 days, for example). Having observed no such transit events, we can thus state, with a confidence of better than 90%, that there are no planets significantly larger then 3Rein coplanar orbits of 60 days or less around the CM Dra system. It should be noted that-for the derivation of a unique period and epoch of a planet, by transit measurements alone-at least 3 transit events need to be identified in the lightcurve. Also, in Section 4, it will be shown that there is a close relationship between the number of transits, Ntr,of a particular candidate and its intrinsic detection probability pi.

Figure 1. a) The probability po(Ntr), that just Ntr transits from a planet are in our observed lightcurve. (After a certain amount of coverage, for example, the probability of having only one transit goes down, etc.) Curves are labeled with the period range of the planets. The probabilities po where derived from the insertion of 60000 planets with random periods and epochs into our data.
b) The cumulative probability
po(Ntr
>= Ntr,min),
that Ntr,min or more transits
from a planet are in our observed lightcurve. For example, for planets
with periods between 20 and 30 days, the probability that there are 3 or
more transits in our data is about 0.79; whereas for planets with periods
of less than 10 days this probability is better than 0.99.
For an estimation of the effect of additional observations, or of the effect of taking subsamples from the observed data (such as a subsample consisting only of the highest precision photometry) on the transit coverage, the following relationship between po, Ntrand T(time of coverage) can be derived:
po(Ntr,1, T1) ~ 1/k po(Ntr,0, T0) (2)
where k = T1/T0 and Ntr,1 ~ k Ntr,0 (of course, Ntr can only take integer values). A doubling of the observing time therefore approximately doubles the number of observed transits, as might be expected.
3. The Photometric Transit Detection Algorithm (TDA): A Matched-Filter Approach
In this section we outline a procedure for the detection of planetary transit signals near the photometric noise in the light curves of eclipsing binaries. Although the application in this paper is specific to the CM Dra system, this method is generally applicable to the detection of such signals in any light curves from eclipsing binaries, or even single stars.
The procedure for instituting the TDA is as follows. First, mutual eclipses of CM Dra are removed from the observed light-curve by the subtraction of a model-eclipse. The light-curve is then converted to relative flux values, D(ti) = DeltaF/Fo, where the zero-point, Fo, is the average off-eclipse brightness of (in this case) CM Dra, and DeltaF is the difference in the flux from CM Dra and the flux from the non-variable comparison stars in the field (TEP1). However, some residuals from nightly extinction variations are still contained in D(ti).
For a transiting test-planet with radius R, period Pand epoch E, a model transit light curve Mp(ti,R,P,E) is generated that describes the relative brightness variations of the star in the presence of a test planet, at all times ti , where observational data have been taken (Fig. 2). It should be noted that Mp(ti,R,P,E) = 0 except for the set of times, ttr , when a transit occurs. Due to computing constraints, circular orbits are assumed in all planet models and orbital effects due to tidal precession (as well as non-central potentials, tides, or general relativity) are also not presently included.
Two fits are now performed on lightcurve data D(ti) which lead to a comparison of the cases `no-transit' and `transit present from model Mp':
re(ti) = | D(ti) - fe | (3),
with the residuals for the planet-being-present case,
rp(ti,R,P,E) = | (D(ti) - Mp(ti,R,P,E)) - fp | (4).
This is performed through the calculation of a statistic k:
k(ti,R,P,E)=[re(ti)-rp(ti)][ti+1 - ti] if ti+1 - ti <= 10 min (5a)
k(ti,R,P,E)= 0 if ti+1 - ti> 10 min (5b),
where sD is the rms of one night's observational data D(ti). The distinction between Equation (5a) and Equation (5b) assures that `holes' in the lightcurve of more then 10 minutes duration are ignored. The scaling by (ti+1 - ti) in Eq. (5a) was needed to account for the various time-increments that appear in sections of the lightcurve originating from different telescopes (See Table 2 in TEP1 for exposure times and duty cycles of the different telesocpes). (We do not use a chi-square statistical form as, conservatively, we do not want to weight outlying points too lightly.) If Equation (5a) applies, then:
k(ti) < 0 when re(ti) < rp(ti) (6)
This is the normal case, when no transit is apparent in D(ti), and fe fits better than fp . The other case is:
k(ti) > 0 when re(ti) > rp(ti)(7).
In this case, fp
is a better description of the data than fe,
which means that the data could contain a transit event at time ti.
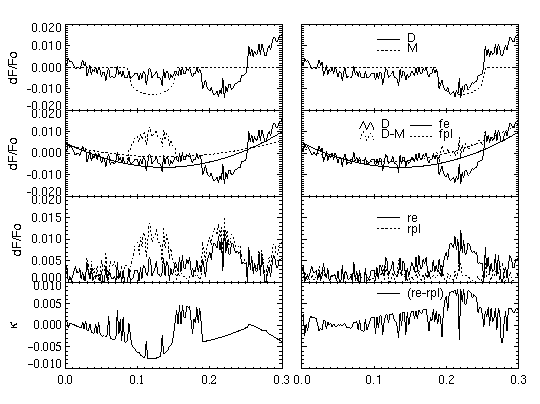
Figure 2. Derivation
of the coefficient k(ti).
The uppermost panels show a nightly lightcurve D (solid line) and
a test model Mp
(dashed line). In panels on the left, Mp
aligns with a range of unconspicous data, whereas in the right panels,
Mplines
up with a possible transit in the data. The second row of panels shows
again the lightcurve D (solid jagged line), and the subtraction
of the model, D- Mp
(dashed jagged line). Overlaid are fe
(the fit to D; smooth solid line) and fp(the
fit to D- Mp; dashed
smooth line). The third row of panels shows the residuals re
(solid line) and rp(dashed
line). In the bottom panels the difference of the residuals, k =re
-
rp, is plotted. It can be
seen, that in the `planet-absent' case (left panels) k(ttr)<
0, and in the `planet present' case (right panels) k(ttr)>
0 at the times where
rp<
re.
In Figure 2 we show the derivation of the transit statistic in the cases of a poor (left panel) and a good (right panel) transit model fit to the light curve data. One can see that the poor fit will result in negative values of the transit statistic while a good fit will give positive values; the higher the value of the transit statistic the better the candidate model fit.
The final `complete transit statistic' C of a given planet model transit is then obtained by a summation of the k(ti) of all points of the lightcurve (though only nights with transits of the model planet have to be considered) with:
C(R,P,E)
=![]() (8)
(8)
The complete transit statistic, C,is hence a normalized (by the rms of each night) indication of the difference in area under the lightcurve (units: DeltaF/Fo x time) between the model-present and `no-model' fits. This linear scaling in the difference of the areas was preferred over a quadratic (c2) one due to the lower weighting that is given to outliers. This procedure to calculate C(R,P,E) is also insensitive to brightness variations with frequencies of >= 4 hours, such as might result from differential extinction or from partial phases of starspot rotation. It is also insensitive to the setting of the zero-point for the light curve data. This is an important point for evaluations of transits that last a large fraction of an observing night, i.e. where a zero-point of the light curve cannot be reliably set. Very long transit events-i.e. ones that begin before the start of a night's observations and end after the end of observations (these occur if the planet transit occurs simultaneously with a binary eclipse, see Fig. 1 in TEP1)-will not, however, be included in the detection. For detached systems, such long transit events are much rarer than the shorter transits, which are about 50 minutes in duration. By excluding long transits, then, we are taking a conservative detection limit approach. An advantage of this method is, however, that C(R,P,E)is sensitive to the best match of the shape of an observed lightcurve to a model transit, as well.
Keeping the test planets' radius R constant, values for the transit-coefficients are then calculated scanning through a grid of values of E and P, with a two-dimensional array of values C(E,P) as the result. Exploratory scans across small sections of the (E,P) parameter space were performed for planetary candidate radii of R = 2.0, 2.5, 3.0, and 4.0 Re , in order to evaluate the detection statistics. The only complete scans through the entire parameter-space were then performed for periods from 7 to 60 days, for a planetary radius of R = 2.5 Re. (The justification for choosing R = 2.5 Reis given in Section 4 on detection statistics. )
The possible planets' epochs, E, are searched completely, if C(E,P) is calculated between an arbitrary initial epoch Eo , and Eo+ P(we used Eo= JD 2450000.0). In order not to miss any transits, the step sizes for the epoch and the period must be (after Jenkins et. al., 1996):
DeltaE = td fov (9)
and
DeltaP = P td fov /tj (10)
where td is the typical duration of a short transit (we used 0.02777 days = 40 minutes), fov is an overlap factor between adjacent scans (we used fov = 0.5), and tj is the time-difference between the first and the last point in the lightcurve. For the light-curve from observations between 1994 and 1998, with tj =1526 days, about 4 x 108 values of C have to be calculated to completely scan for all distinguishable transit models from planets with periods from 7 to 60 days. Considering that each value of C is the result of the summation in Equation (8), it is obvious that the problem is computationally very intensive, and would have normally required about 2 years of CPU time on a current high performance work station.
To reduce the computational load, we divided the light-curve into 5 yearly sections, each of which covered a time-range of less then 200 days (CM Dra was observed only within the 7 months of March through September in each year). Thus, without missing any transits within the same year, DeltaP could be incremented with larger step sizes, based on each year's tj = 200 days (Equation 10). Therefore, the length of the yearly light-curve that had to be considered-i.e. the number of points in the summation Equation (8)-was decreased to about a fifth of the previous number. However, there were now 5 scans made, one for each year, which created 5 arrays C(E,P) with identical dimensions. The total savings in computing time was thus 1526/200 or a reduction factor of about 7.5, making it possible to perform the complete calculation in about 2 months using 2 workstations, with an optimized code that allowed us to perform about 30 planet-model evaluations per second. These five scans covered the period range with 30,917 steps at period-increments between 4.8 x10-3 and 4.2 x 10-3 days and covered the epoch with increments of 0.014 days, for a total of 5.6 x 107 planet model scans being performed altogether. An additional advantage of this partitioning of the light-curve is, that it became possible to add in data from future observations so that only the additional data would need to be evaluated.
However, such savings in computational time did not come without some cost. Consider a planet with an intrinsic epoch and period, (Ep, Pp), that has caused, for example, 4 transits, two of which were observed in 1994 and two of which were observed in 1997. In order not to miss the alignment between all 4 of them, the scans would have to be performed with the step-sizes given by Equations (9) and (10), (based on tj = 1526 days). The scans for the individual years, with tj = 200 days, are only sufficiently fine to find any alignment between transits within that same year. Thus, in 1994, there will be a local maximum, C94 (Ej, Pk), (where j and k are the indices in the array spanning E and P). The position of this maximum at (Ej, Pk)will be within DE/2 and DP/2 of the intrinsic values Ep and Pp. The scan for the year 1997 will now also find a maximum, C97,which is also constrained to be within DE/2 and DP/2 of Ep and Pp, but may well lie on the neighboring array elements j±1 and k±1, relative to the position of C94. The transit-coefficient arrays from the individual years cannot, therefore, be directly added, since some planet candidates would thereby get lost.
An adding algorithm was therefore developed, which extends all local maxima of C to their neighboring pixels in the yearly arrays, before adding the yearly arrays to an array describing the whole observations, that is C94-98. This adding algorithm thus assures-for a planet with parameters (Ep, Pp) that would have caused a value of Cmax in a very fine scan-that there will be a similar value, Calarm(Ej, Pk), in the whole-observational array C94-98 within a range of one array element of the intrinsic parameters (Ep, Pp). This 'neighborhood adding', used to obtain C94-98,, may however, also promote unrelated events from the different years to cause local maxima in C94-98. Values of Calarm(Ej, Pk) in C94-98 are therefore only upper limits to a Cmax that might be found with a much finer scan of the whole light-curve.
Final high-time-resolution evaluation scans were therefore performed, testing the regions within a neighborhood of two array elements around all local maxima Calarm, with a very fine grid (here we used tj = 1526 days and fov = 0.5), the result of which was Cmax, the final maxima found in the whole light curve. To find all planet candidates with Cmaxlarger then some threshold Cthres, it was therefore necessary to scan C94-98in fine grids around all local maxima where Calarm > Cthres. To find the best planet candidates, while assuring that none were missed, it was necessary to scan fine grids around the 5000 best values of C94-98. The resultant 9 best candidates are given in Section 5 on detection results.
In order to determine a reasonable threshold Cthres for transit candidates found by the TDA, we turn now to a description of our TDA in terms of standard detection theory.
4. The Matched-Filter in Terms of Signal Detection Theory
The procedure for transit signal detection, as described in the previous section, is based on the matching of all possible planetary transit models against our differential light curve. The quality of these matches is numerically described by the transit statistic, C, which is our correlation statistic. The set of these transit statistics, resulting from testing against all possible planetary transit models, constitutes the statistic of detectability for a given sized transiting planet in our observational light curve data.
The detectability of a planetary transit signal can be pictured as the result of two hypotheses: Ho, the null hypothesis (no signals of planetary transits are present) and H1, the detection hypothesis, that is, planetary transits are present in the light curve (see Jenkins et. al. 1996, after Van Trees 1968). For the null hypothesis, Ho, we have used the set of all statistics C(E,P), which were generated directly from the statistical test of our light curve data against possible model-transits, as described in the previous section. This set may contain one, but never more then very few, real planets. However, the number of real planets is, in any case, negligible when compared with the number of all possible distinguishable (with respect to the transit-pattern they cause) planet-transit models. We found the number of distinguishable planet-transit models to be about 4 x 108 for our observational data coverage (see Section 3).
The H1 hypothesis was generated by adding planetary transit models M(ET,PT) to our data, and then obtaining the statistics C(ET,PT)for these modified data, (where ET, PT indicated the parameters of the model planet). The set C(ET,PT) for the H1 hypothesis was calculated using 10,000 random values of ETand PT .
Different H0 and H1 hypotheses can, of course, be generated for planets of different sizes, or for different ranges of periods, or from different subsamples of the CM Dra lightcurves. In all cases it is important, however, that the same assumptions are used for both the H0 and H1 hypotheses. In Figure 3 we show a histogram of the distribution of a null hypothesis H0 and a detection hypothesis H1. The horizontal axis is the detection statistic (the values of C in the cases H0 and H1), while the vertical axis indicates the distribution of these values (normalized to 1). The separation of the H0 and H1 curves represents the detectability of, in this case, a planetary transit signal of a given size within the observational noise of the differential light curve. The separation of H0 and H1 will increase as the signal-to-noise increases.
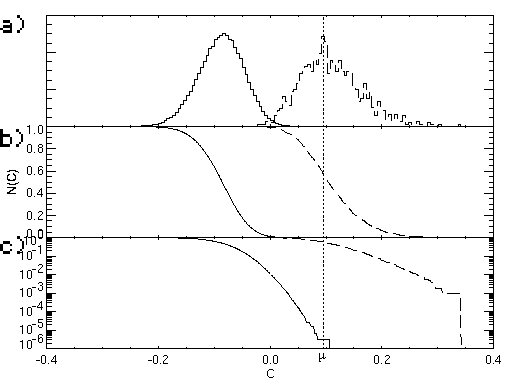
Figure 3. a) A sample H0-H1 plot showing the histogram (normalized to 1) of the distribution of the detection statistic given by the set of values C . The overlap of the planet-absent hypothesis, H0, with the planet-present hypothesis, H1, determines the detectability. (In this example, of many possible examples, we show H0 andH1 diagrams from correlations against model planets of size 2.5 Re, with periods between 7 and 10 days, which have caused 7 transits in the lightcurve)
b) The same as a), but H0 and H1 are plotted in reverse (starting at highest value) cumulative histograms.
c) The same as b),
but on a logarithmic scale that better shows the smallest values of H0
and
H1
.
A
threshold m is set where the values of H0
are
smaller than 10-6
(solid line). From the corresponding value H1(m)
>=
0.1in
b) one can see that the intrinsic detection probability pi
of a planet corresponding to these distributions of H0
and H1 is about
0.55.
A threshold of detectability, m, can be selected in between the two hypotheses, and will determine the intrinsic detection probability pi, (referred to in Equation 1), and the false alarm rate, fA. The area to the left of m, yet still under the H1 curve, is the probability of having missed a real planetary transit event that was in the data, (i.e. 1-pi.). The value of 1-pi can be read off from the value of H1 at m in the reverse cumulative histogram, which is an alternative way of plotting the detection hypothesis, H1(m) = pi (Figures 3b and c). The goal of any signal detection scheme is, of course, not to miss much, while nevertheless simultaneously reducing the probability of false alarms to as low a value as possible.
To the right of the threshold m, where H0 overlaps H1, the null hypothesis has values that fall within the signal-present area, i.e. within H1. The ratio of the area of H0 to the right of m, to the total area of H0 (in Figure 3a), defines the false-alarm rate fA, which describes the ratio between the number of false alarms and all cases of H0, that is, the probability that any arbitrary point in (E,P) parameter-space is a false alarm. In the cumulative histogram (Figures 3b and c) therefore: fA = H0(m). The relation between pi and fA is shown in Figure 4, (although it can also be read off from Figures 3b and c). Since H0 contains about 4 x 108 distinguishable cases in (E,P)parameter-space (see Section 3), fA needs to be exceedingly small to get the number of false alarms as small as possible (without missing any transit signals that could have shown up in the data). The value of m was therefore chosen to produce a very small number of alarms, - small enough to allow subsequent verification of the nature of each individual alarm observationally (Section 5, below). In the determinations of the intrinsic detection probability pi cited later, we set m so that fA = H0(m) ~ 10-6, that is, our false alarm rate was less than about one in one million.

Figure. 4. The
relation between the intrisic detection probability pi
and
the false alarm rate fA.
This figure is based on the same data-set as in Figure 3.
The values of C(E,P) that were included in the distributions of H0and H1 had to fulfill a further requirement. This is, that the number of transits, Ntr in the lightcurve that are needed to derive a planet candidate's parameters E, P unambiguously is Ntr = 3. Requiring more transits increases the separation between H0 and H1 (Figure 5), and thus increases pi, but will simultaneously decrease po by requiring more events (see Figure 1). In the H0-H1 diagrams of Figure 3, the large numbers of models that create the H0and H1 distributions have been separated by the number of transits (Ntr) they contain, showing a strong dependency of pi with Ntr.
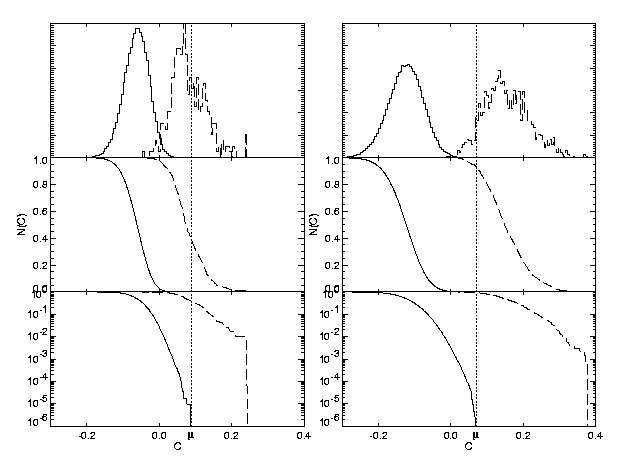
Figure 5. H0-H1diagrams
similar to Figures 3 for a specific planet model with 2.5 Re.
Here the H0 distribution
is derived from about 5 x 107
values of C calculated in the 'complete' scan of (E, P)
parameter
space (see Section 3). The H1
distribution is obtained from the insertion of 10000 test-planets with
random parameters (E,P) into the lightcurve. From this large number
of models, for a) those with
Ntr
= 5 have been selected, giving pi ~
0.35 ± 0.05, and for b) those with Ntr
=10, giving pi ~
0.92 ± 0.03.
If Ntr is kept constant, the intrinsic detection probabilities pi depend strongly on the planet's size, but are nearly independent of the planet's period. This is a consequence of the duration of the transits being only weakly dependent on the planetary period. Similarly, the observational detection probability po varies strongly with the period, but is nearly independent of the planet's size, since the frequency of the transits is independent of the size, and the duration of the transits is affected in a minor way only, varying on the order of (R +R*)/R*, where R*is the star's radius. Therefore:
pi =pi ( R, Ntr) (11)
(see Figure 6) and
po =po ( P, Ntr) (12)
(see Figure 1a), i.e. pi is only a function of the number of transits and of the transiting planet's radius, while po is only a function of the number of transits and of the planet's orbital period.
In a way similar to Equation (1), which gives the total detection probability pd for a single candidate, the total detection probability for any candidate (which may appear with any value of Ntr) can be obtained by:
pd(R,P)
= ![]() (13)
(13)
The values of pd
, for planet sizes between 2 and 3Re,
that were thus obtained from the analysis of our CM Dra lightcurve are
shown in Figure 7.
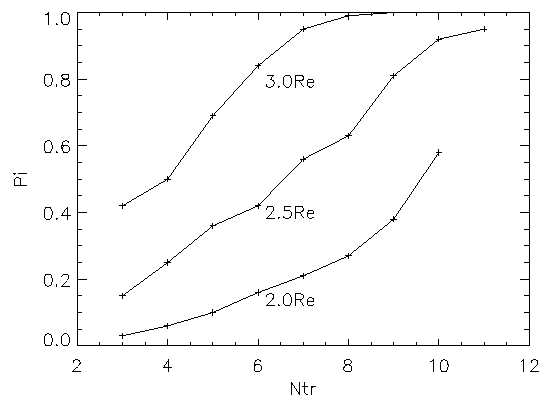
Figure 6. Values
of pi
=pi
(
R,
Ntr) for
R= 2.0, 2.5
and 3 Re. All individual
values have been derived from H0-H1diagrams
as shown in Figure 4. Values of pi
for
2.5 Re are based
on the 'complete' scan of (E,P)
parameter space (5 x 107
values of C ), whereas the values of pi
for
2.0 and 3.0 Re
are based on 'exploratory' scans through epoch-limited regions in (E,P)
parameter
space, with H0
distributions derived from about 4 x 105
values of C .
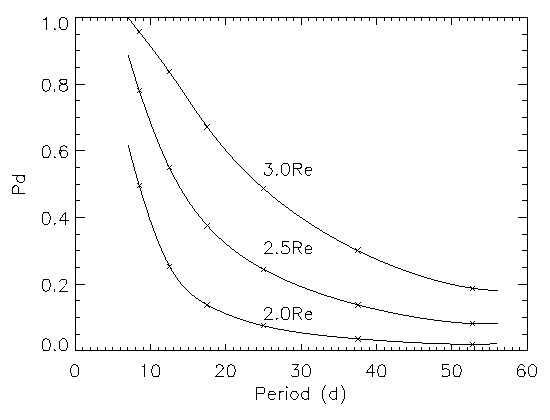
Figure 7. Values
of pd
(R,P)
for
R=
2.0, 2.5 and 3 Re
obtained
from the summation in Equation (11). These values represent the final detection
probabilities (a product of the photometric noise-limited precision, pi
, and the observational coverage, po
) of planet candidates contained within the TEP lightcurve of CM Dra for
the observational years 1994 through 1998.
5. Detection Results of the TDA Analysis of the CM Dra Light Curve
5.1 Size Limits of the Detection Algorithm
In TEP1 we reported that no obvious transits for planets much larger then 2.5Re had been seen in the lightcurve. However, they cannot be excluded entirely, as can be seen from the values of pi for 3Re (Figure 6). On the other hand, 2Re turned out to be too optimistic a detection goal with the current data set size and precision. As can be seen in Fig. 6, at least 10 transits are needed from a 2Re planet to obtain over 50% detection probability within the current data. Using a 'Class 1' subset of about 35% of the full CM Dra lightcurve, consisting only of the best nights' data (requiring an rms of less then 0.4%), values of pi for 2Re similar to the ones reported for 2.5Re with the full lightcurve were obtained. Unfortunately, with the coverage by 'Class1' data being much smaller (340 hours), the observational detection probability po is too low to maintain 2Re as a realistic detection goal. An exception may be 2Re planets with very short periods of less then 10 days, where detection probabilities approaching 50% could be obtained. For the complete TDA scan of the (E,P) parameter space, which was computationally very intensive, we then choose planet models based on a size of 2.5Re. Since the TDA algorithm of Section 3 is sensitive to transits in the data caused by any planets larger than the 2.5Re model planets, we thereby did not preclude the discovery of larger planets. (But again, any transiting planet significantly larger than 3 Re should have been very obvious in the lightcurve, and its detection probabilities, which are governed by po alone, would be very high (see Figure 1b for Ntr,min = 1).
After constraining the optimum signal strength (i.e. planet size) to 2.5 Re then, the full scan through E and P for periods from 7 to 60 days was performed for such planets, (requiring a total of 5.6 x 107 planet models to be evaluated, as explained in section 3). We note that the median precision of our photometry, about 0.45%, corresponds to a single, central transit depth of a 2.6Replanet around CM Dra, (that is, the TDA for a 2.5Re planet has been operating at approximately the noise limit for one transit event). Because of the large, but still limited, data set as well as good, but limited, photometric precision, the TDA will not have been very sensitive to transits caused by planets smaller than about 2.5Re,. For smaller planets, either data with lower noise would be needed (such as the `Class 1 data' mentioned above), and/or significantly longer observational coverage.

Figure 8. Each
graph shows a barycenter crossing were the 8.16-day period candidate (solid
line) would have caused transits in the observed lightcurve (crosses).
The horizontal axis gives the time in Julian Days, the vertical one the
brightness variation
DeltaF/Fo.
The 8.16-day candidate would have had the most transit events in the lightcurve
between 1994 and 1998 (11 barycenter crossings; 14 whole or partial transit
events altogether). In 1999, observations at three nights to verify this
candidate showed a negative result (last 3 graphs in lower right)

5.2 Evaluation of Candidate Planets
As a result of the search for maxima in the C(E,P) array (See Section 3), nine top planetary transit candidates of various periods, (but all with a preliminary size of 2.5Re), were determined from the data taken through 1998. The period of these candidate planets, their binary-barycenter-crossing epochs, the value of the final transit-coefficient, and the number of transit events in the lightcurve, are given in Table 2. These are the best transiting 2.5 Re planet models selected from 400 million possible period-epoch candidates. (A few further ones were rejected since they depended on one dominating attenuation event, or on events from only one observatory, both of which might be suspect.) Figures 8 and 9 show the attenuations in brightness in the light curve that have been fit with the model transits for the 8.16-day candidate (the one with the highest number of transits) and for the 22.57-day candidate (the one that `survived' after the observations in summer 1999; see Section 6). It is important to note that these candidate planetary transit events are clearly very close to the observational noise. In case of point, there have to be top candidates in any such extensive search in the observational noise, and one would hope for one -or very few- clearly outstanding candidates. However, the complete transit statistic of these nine candidates were only about 10-20% above those of the next possible candidates. Given a field of over 400 million possible models, some distinguished, yet arbitrary, candidates may emerge. Hence the necessity of predicting and observationally confirming such candidates (see discussion in Section 5.3 below).
Table2. Top Planetary Transit Candidates from Observations in 1994-98, and 1999
| P(days) | E+JD2450000 | Ntr(1994-98) | C(1994-98) | Ntr(1999) | C(1999) |
| 7.67 | 6.86 | 8 | 0.109 | 1 | -0.014 |
| 8.16 | 2.15 | 11 | 0.129 | 3 | -0.039 |
| 8.83 | 8.81 | 8 | 0.129 | 2 | -0.014 |
| 10.12 | 5.35 | 5 | 0.144 | 1 | -0.033 |
| 12.03 | 8.08 | 9 | 0.149 | 3 | -0.012 |
| 19.85 | 14.56 | 5 | 0.129 | 2 | -0.017 |
| 20.56 | 19.94 | 7 | 0.129 | - | - |
| 22.57 | 13.77 | 6 | 0.116 | 1 | 0.004 |
| 26.44 | 2.31 | 5 | 0.124 | - | - |
As an additional note, when looking for transit events across eclipsing binaries, one must be aware of the binary orbital frequencies' contribution to photometric variability and thus of planetary orbital periods that are modulo to the binary period. Candidates two and three in Table 2 above (periods of 8.83 and 10.12-days) are within a few percentages of being modulo to CM Dra's period of 1.268 days. However, upon inspection, none of the photometric attenuation events that led to these candidates' high transit statistic shared any nearby sequential phase events with possible rotating features that might have been caused by photometric variations on the surface of CM Dra A or B. We note however, that the periods of several of the planet candidates among themselves are related by multiples very close to integers (such as 8.83d : 19.85d : 26.44d ~ 4 : 9 : 12); i.e. they may share several of the same transit events.
5.3 Predicted Transit Detection Statistics and Observational Confirmation
While the product of the probability of the transit being in our light curve po, with the signals of a given candidate having enough transit power ("energy" in signal detection nomenclature) to be detectable pi, determines the total transit detectability, pd, of a given candidate (Equation 1), the confidence level in such candidates as being of a planetary transit nature can only be reliably estimated by the detection of a predicted transit event signal (i.e. a significant drop in stellar brightness "on schedule". This detection confidence is due to the low probability that at the predicted time a transit signal, of the correct duration in the lightcurve, will be present that will increase the coefficient C of the predicted individual candidate.
As previously stated, it is essential that the number of predicted candidates be kept relatively small. If a very large number of predicted candidates is to be verified, any attenuation in a future observed lightcurve (that is, any feature in the lightcurve that may lead to sufficiently high values of k; see Equation 5) could be assigned to at least one of very many candidates, thus invalidating the use of an observational prediction as a tool to assess the reliability of any detection.
The probability that the prediction for a single candidate is valid can be estimated as follows. In our whole observational lightcurve, about 3% of the coverage data points cause positive values of k for transits lasting about 50 minutes (which is the most common kind of transit). Another way of stating this is, that about 3% of the lightcurve displays some feature (i.e. a series of points below the mean) that could be some kind of transit (remember that we are largely working at the mean photometric noise level). In this, the nature of each transit feature is assumed to be unknown-it may be a transit from a planet, but could also be due to observational photometric variability of any kind (as discussed in TEP1). The probability that, at a particular predicted time, a feature that may be a transit shows up, is therefore about 3%. This means, that if such a feature is being observed at the predicted time, there is a 97% confidence that this feature is related to (i.e. caused by) that predicted transit event-i.e. 1 minus the false alarm rate for a random transit event. We note that the specific value of 3% holds, of course, only for photometric data of the approximate quality as the data obtained in our observations, and will, of course, be smaller for data with lower noise.
Since we looked for seven candidates 13 times and found one possible surviving candidate out of 12, our confidence in this candidate is one minus the probability that this could have happened randomly, that is: 1 - (0.97)12(0.03)(13) = 73%. Similarly, if the same planet candidate causes n further observed transit events at the correctly predicted time, the probability of a false alarm is determined by:
PfA = (0.97)12(0.03)(13)(0.03)n(14).
The probability of false alarm for additional observations is thus 0.81%, 0.024%, 0.00073%, and so on, with the confidence in a detection increasing rapidly beyond 99% with additional predicted transit events of the 22.57-day candidate.
Clearly keeping the number of candidates that are to be tested by such predictions small is needed to validate these predictions. Fortunately, the predicted transit times for the candidates listed in Table 2 are almost entirely independent of each other in the sense that almost no predicted transit times for any candidate overlap. Thus, Equation 14 will most closely apply to the estimation of the detection confidence resulting from our predicted transit events of the individular candidates given in Table 2.
6. Observations of Predicted Candidate Planets
6.1 Observations
Once specific candidate planets have been determined, specific follow-up observations based on the calculated ephemerides of transits can be performed. Ephemerides were calculated for the candidate planets listed in Table 2 and thirteen predicted transit events, belonging to seven of the nine candidates, were observed at Lick Observatory in summer 1999. The 20.56d and the 26.44d candidates could not be observed due to bad weather at the predicted times. For all of these observed planet candidates, resultant transit statistics were subsequently calculated for the observations in 1999. Results are included in Table 2, along with the number of predicted events covered, and the transit statistic obtained in 1999.
In the case of the 8.16-day candidate- which had 11 previous suspected events- three predicted transit times were observed (Fig. 8). However, each of the three observations resulted in a negative transit statistic , thus nullifying this candidate. This case may be the most extreme, but to some extent-with so many possible candidates (over 400 million searched near the noise level)-it can perhaps be understood that there is a non-vanishing probability that even good candidates may be consequences of random sequences of transit-like features. Again, this emphasizes the importance of predicted transit events and follow-up observations before a definitive small planet detection (i.e.one near the observational noise) can be reliably claimed. Four more planet candidates were ruled from the observations of one to three predicted transits. Only the 22.57-day period candidate (Fig. 9) showed a positive transit statistic from the one predicted transit that was observed.
In summary, in this work to date we have taken the highest nine candidates isolated from other possible planets in epoch and phase by the TDA. However, in the case of CM Dra, the resultant candidates were neither very far above the observational noise nor significantly (< 20%) above many other candidates. Nevertheless, the "surviving" candidate (with the 22.57-day period transit signature) will need to be observationally confirmed or ruled out to be definitive. As discussed in Section 5.3 above, the confidence in such a candidate should grow as Equation (14) indicates, with the specific percentage of 3% being dictated by the photometric noise of the observational program. Observational confirmation of the 22.57-day candidate will therefore be a high priority.
7. Discussion
The binary nature of our target stellar system introduces several complications for planetary transit detections when compared to the detection of planetary transits around single stars. For example, we had to remove the mutual binary eclipses and also calculate, for a specific model, M(E,P), each configuration of E and P. Beyond these differences, however, the method outlined here should be applicable to detecting transits around most kinds of stellar systems. In the case of a planet transiting a single star, a model, M=M(P,i), can to be calculated only with reference to the period, (and the inclination - if desired), where P only weakly affects the duration of the transit-but not its shape-and i affects mainly the amplitude. Independent of the details of how the coefficient C is precisely derived, the determination of the detection probability and the false alarm rate using the H0 and H1 hypothesis can be applied. We expect even for space-based transit observations (which would have observational coverage of much higher uniformity), that an analysis of the dependence on the number of transits (Ntr) of the model planets, similar to the one outlined here, will also have to be performed.
Detection of photometric variations due to transits is presently the only repeatable method for the investigation of possible extrasolar planets around close binaries that we are aware of-the binary nature of these systems making them, at present, too complex to study for minute radial velocity variations, for example. However, in the photometric case, the quasi-periodicity of the expected variation actually helps to establish a more unique series of transit signatures, generally allowing one to rule out more periodic events of intrinsic stellar variability. In addition, for ground-based observations, binary transit events can generally be expected to contribute their power at higher frequencies (50 minute transits versus several hour-long transits) and thereby be more easily separable from the higher-amplitude low-frequency observational noise (see Doyle et. al. 1996, TEP1).
At present there seem to be no compelling reasons for arbitrarily excluding close binary systems as sites of planet formation. Stability considerations (Donnison and Mulkulskis 1992, Holman and Wiegert 1999) as well as discoveries of circumstellar material (Jensen et al. 1996, Kalas and Jewett 1997, as examples) rather indicate that close binaries could be active sites of planet formation. With the discovery of a jovian-mass planet around Gliese 876 (Marcy et al. 1998) clearly there also seems to be nothing intrinsic to M-stars that would exclude planet formation around them (although stellar populations of differing metallicities could easily be seen to produce significant differences in planetary formation rates). Recent atmospheric models, as well, have not excluded smaller, inner M-star planets as potential sites of liquid water (Haberle et. al. 1996, Joshi et. al. 1997, Heath et. al. 1999).
8. Conclusions
We have performed a search for terrestrial-sized planets around another main-sequence star system, reaching a planet detection limit of 2.5Re (i.e., about 1% the size of Jupiter). While we have observed one of the smallest known eclipsing binaries, CM Dra, we have also used only 1-meter-class ground-based telescopes. Clearly this method may be extended to more crowded stellar fields (many simultaneous targets; Doyle et. al. 2000) as well as to larger stellar systems. In the case of larger eclipsing binary systems, one may expect the photometric precision to improve both with the square-root of the light gathering power of the telescope, as well as with the significantly decreased scintillation noise that can be expected from larger telescopes (Dravins et. al. 1998, for example).
Whether the current planet candidate turns out to be a true detection or simply a photometric noise artifact, the methodology outlined herein has hopefully demonstrated the validity of pursuing the detection of small inner (i.e., terrestrial-sized) planets around late-type main-sequence stars using the transit/matching algorithm methodology with existing observational facilities. This method should also find application to near-term spacecraft missions, as well. This may be the best way to at least begin to answer that most intriguing of planetary detection questions: "Are there other `Earths'?."
9. Acknowledgements
LRD wishes to thank the SETI Institute
for a special observing grant, and the University of California, Lick Observatory
allocation committee for continued substantial time on the Crossley telescope
(incidentally the oldest professional-sized reflecting telescope, first
silvered in the late 1870s; see Stone 1979). HJD acknowledges a grant `Formación
de Personal Investigador' by the Spanish `Ministerio de Educación
y Cultura' for the years 1997 and 1998. The IAC80 and OGS telescopes are
operated at Izaña Observatory, Tenerife by the Instituto de Astrofísica
de Canarias. Capilla Peak Observatory is operated by the Institute for
Astrophysics of the University of New Mexico. (The contributions of the
other previously participating observatories for the years 1994 through
1996 are given in TEP1.)
References
Brandmeier, S. and L.R. Doyle, 1996, in Circumstellar Habitable Zones: Proceedings of the First International Conference, L.R. Doyle (ed.), Travis House, Menlo Park, Calif., 251.
Deeg, H.-J. 1998, in Brown Dwarfs and Extrasolar Planets, R. Rebolo, E. L. Martin, and M.R. Zapaterio-Osorio (eds.), A.S.P. Conference Series 134, San Francisco, California, 216.
Deeg, H.J., L.R. Doyle, V. P. Kozhevnikov, E. Martin, B. Oetiker, E. Palaiologou, J. Schneider, C. Afonso, E.T. Dunham, J.M. Jenkins, Z. Ninkov, R. Stone, and P.E. Zakharova 1998, A&A, 338, 479 (TEP1).
Deeg, H.J., L.R. Doyle, 2000, in Proceedings of Extrasolar Planets Photometry Workshop, 1998 at SETI Institute, Mountain View, CA., W. Borucki and D. Koch, (eds), in press.
Deeg, H.J., Doyle, L.R., Blue, J.E:, Martin, E.L., Rottler, L, Schneider, J. 2000, submitted to A&A Lett.
Deeg, H.J., Martin, E.L., Doyle, L., Jenkins, J., Schneider, J., Chevreton, M., Palaiologou, M. 1997, A&A Trans., 13, 233.
Donnison, J.R. and D.F. Milkulskis, 1992, MNRAS254, 21.
Doyle, L.R., L. Rottler, H.J. Deeg, J.E. Blue, and M. Navaarate, 1999, in Bioastronomy: A New Era in the Search for Life in the Universe, (G.A. Lemarchand, ed.), in press.
Doyle, L.R., H.J. Deeg, J.M. Jenkins, J. Schneider, Z. Ninkov, R. P.S. Stone, J.E. Blue, H. Götzger, B, Friedman, and M.F. Doyle, 1998a, in Brown Dwarfs and Extrasolar Planets, R. Rebolo, E. L. Martin, and M.R. Zapaterio-Osorio (eds.), A.S.P. Conference Series 134, San Francisco, California, 224.
Doyle, L.R., E.T. Dunham, H.J. Deeg, J.E. Blue, and J.M. Jenkins, 1996, J.Geophy.Res. (Planets)101, 14823.
Dravins, D., L. Lindegren, E. Mezey, and A.T. Young, 1998, PASP 110, 610.
Gilliland, R.L. and T.M. Brown, 1992, "Limits to CCD Ensemble Photometry Precision, and Prospects for Asteroseismology," PASP 104, 582.
Haberle, R.M., C.P. McKay, D. Tyler, and R.T. Reynolds, 1996, in Circumstellar Habitable Zones: Proceedings of the First International Conference, L.R. Doyle (ed.), Travis House, Menlo Park, Calif., 29.
Hale, A. and L.R. Doyle, 1994, Ap&SS 212, 51.
Heath, M., L.R. Doyle, M. Joshi, and R.M. Haberle, 1997, Origins of Life 29, 405-424.
Hertz, P., K.S. Wood, and L. Cominsky, 1995, ApJ438, 385.
Holman, M.J., and P.A. Wiegert, 1999, AJ117, 621.
Jenkins, J.M., L.R. Doyle, and D.K. Cullers, 1996, Icarus119, 244.
Jensen, E.L.N., D.W. Koerner, and R.D. Mathieu, 1996 AJ111, 2431.
Joshi, M.M., R. Haberle, and R.T. Reynolds, 1997, Icarus129, 450.
Kalas, P. and D. Jewitt, 1997, Nature386, 52.
Lacy, C.H., 1977, ApJ 218, 444.
Marcy, G.W, Butler, R.P., Vogt, S.S., Fischer, D., Lissauer, J., 1998, ApJ 505, 147.
Rosenblatt, F., 1971, Icarus14, 71.
Schneider, J., 1994, Planet. Space Sci 42, 539.
Schneider, J. and L.R. Doyle, 1995, Earth Moon & Planets 71, 153.
Schneider, J. and M. Chevreton, 1990, A&A232, 251.
Stone, R.P.S., 1979, S&T, 58, 307.
Struve, O., 1951, The Observatory72, 199.
Van Trees, H.L., 1968, Detection, Estimation, and Modulation Theory, Part I, John Wiley and Sons, New York.
Young, A., R.M. Genet, L.J. Boyd, W.J. Borucki, G.W. Lockwood, G.W. Henry, D.S. Hall, D.P. Smith, S.L. Baliunas, R. Donahue, and D.H. Epand, 1991, PASP 103, 221-242.