Rotation is thought to drive cyclic magnetic activity in the Sun and Sun-like stars. Stellar dynamos, however, are poorly understood owing to the scarcity of observations of rotation and magnetic fields in stars. Here, inferences are drawn on the internal rotation of a distant Sun-like star by studying its global modes of oscillation. We report asteroseismic constraints imposed on the rotation rate and the inclination of the spin axis of the Sun-like star HD52265, a CoRoT prime target known to host a planetary companion. These seismic inferences are remarkably consistent with an independent spectroscopic observation (rotational line broadening) and with the observed rotation period of starspots. Further, asteroseismology constrains the mass of exoplanet HD52265b. Under the standard assumption that the stellar spin axis and the axis of the planetary orbit coincide, the minimum spectroscopic mass of the planet can be converted into a true mass of 1.85 +0.52- 0.42MJupiter which implies that it is a planet, not a brown dwarf.
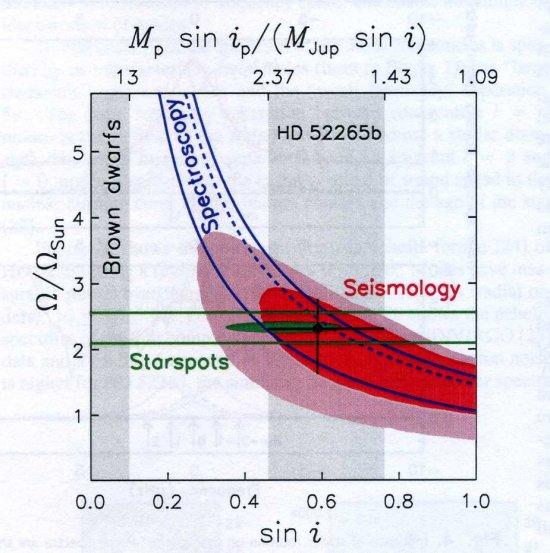
Constraints on stellar rotation and planet mass. The dark-red and light-red regions are the 1-σ and 2- σ seismic constraints on stellar rotation in the plane (Ω / ΩSun) - (sin i), where Ω is the bulk angular velocity, ΩSun / 2 π= 0.424 μHz is the solar Ca
Advertised on
References
Proceedings of the National Academy of Sciences, vol. 110, issue 33, pp. 13267-13271