TEXTOS COMPLEMENTARIOS
Guía de uso - Introducción - Temas principales - Textos complementarios - Experimentos - Física avanzada - Memoria - Bibliografía
4. Gráficos espacio-tiempo
Para describir correctamente lo que nos rodea tenemos que situarnos en el marco de referencia adecuado. Para decirle a un amigo qué es un círculo lo mejor es coger una hoja de papel y dibujarlo. El círculo tiene dos dimensiones espaciales y el papel igual. El plano del papel es el marco adecuado. Si queremos explicarle qué es una esfera, ya no nos sirve el papel. Lo ideal es darle, por ejemplo, una bola de billar que tiene tres dimensiones espaciales y que la toque.
¿Cuántas dimensiones tiene nuestro universo y cómo podemos imaginarlo y describirlo?, ¿cuál es el marco adecuado? Aquí entra Einstein.
Einstein sabía que la luz (y toda radiación electromagnética) se mueve como máximo con una velocidad de 300.000 km/s y se atrevió a proponer (adivinó) que nada en el universo podía superar esta velocidad de la luz. Ésta es la base de su teoría especial de la Relatividad. Pero lo que nos interesa aquí es que, si su teoría es correcta, podemos describir las distancias (las dimensiones espaciales) como tiempos. Podemos decir que un kilómetro es la distancia que recorre la luz en 1/(300.000) segundos, un kilómetro es ese tiempo. Con Einstein nos damos cuenta de que los conceptos de espacio y tiempo están mezclados; que para describir nuestro universo necesitamos las tres dimensiones espaciales más la dimensión temporal, simultáneamente. Lo llamamos el espacio-tiempo de cuatro dimensiones, y, por lo que sabemos hasta ahora, es el marco más adecuado para entender el universo actual.
Aunque podemos entenderlo con ayuda de las matemáticas, es difícil imaginarnos realmente el espacio-tiempo de cuatro dimensiones (los físicos que investigan en ello tampoco pueden hacerlo mucho mejor que nosotros). Nuestros cerebros se han desarrollado por evolución adaptándose a un entorno tridimensional, no cuatridimensional. Visualizar un espacio de cuatro dimensiones es más difícil que explicarle a nuestro amigo la esfera de tres dimensiones con las dos dimensiones del papel; esto último no es imposible (porque nuestro cerebro sí imagina tres dimensiones espaciales) pero no es fácil, y probablemente acabemos echando mano de las matemáticas. Tocando el papel no basta.
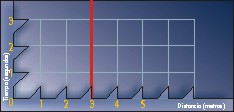
Para entender el espacio-tiempo haremos el problema más fácil, de modo que podamos visualizarlo. Imaginemos que sólo hay una dimensión espacial y que Einstein nos pide que inventemos el espacio-tiempo de dos dimensiones. Entonces dibujaríamos un gráfico donde un eje (por ejemplo, el horizontal) fuera el espacio y el otro eje (el vertical) el tiempo. En el eje del tiempo podemos poner marcas, por ejemplo, cada segundo. Si queremos podemos poner también marcas en segundos en el eje espacial (y cada marca correspondería a una distancia de 300.000 km. Esto puede ser una unidad inconveniente para las medidas de cada día: ¿cuánto mides tú de alto en segundos?). Por ello pongamos marcas normales, por ejemplo, cada metro. Ahora jugamos a poner sucesos reales en este gráfico. Por ejemplo, tú estás quieto a 3 metros de mí. Tu "trayectoria" en el gráfico espacio-tiempo es la línea recta vertical que se muestra en la figura:
En la figura superior, vemos que aunque tú estás quieto, el reloj sigue marcando los segundos, tic-tac, tic-tac... y por eso tu trayectoria es una recta que se alarga a medida que el tiempo pasa.
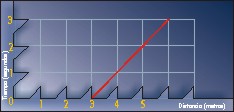
Ahora supón que te alejas de mí con una velocidad de 1m/s. Tu trayectoria en el gráfico espacio-tiempo es una línea recta inclinada así:
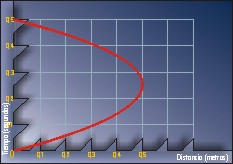
Modifiquemos ligeramente el gráfico, y pongamos en el eje horizontal (el de las distancias) la altura que tienes sobre el suelo (el eje vertical lo dejamos como estaba, el tiempo). Intenta visualizar ahora que si das un salto hacia arriba tu trayectoria en el gráfico espacio-tiempo es una curva llamada parábola (ver figura), supuesto, claro, que hay una fuerza de gravedad que "tira" de tí hacia abajo.
Éste es un resultado muy interesante: las trayectorias en el gráfico espacio-tiempo son curvas cuando actúa la gravedad.
Ahora vamos a ser más valientes y vamos a representar la trayectoria en un gráfico espacio-tiempo de tres dimensiones (ahora serán dos dimensiones espaciales, más el tiempo) de un planeta (por ejemplo, la Tierra) en órbita circular alrededor del Sol. Ya hemos aprendido que el eje del tiempo siempre corre igual, los segundos aumentan monótonamente como dice nuestro reloj, tic-tac-tic-tac... así que la trayectoria de la Tierra en este gráfico es una hélice regular y de sección circular. Para hacer este gráfico (ver figura), tenemos un problema insalvable (describir tres dimensiones en un mundo de dos, el papel) que arreglamos mal que bien como es habitual, con una perspectiva.
Pero lo importante es que vemos de nuevo que donde hay gravedad (la Tierra y el Sol atrayéndose) las trayectorias en los gráficos espacio-tiempo son curvas (no son líneas rectas). Este resultado es la clave para entender la genial idea de Einstein sobre la gravedad: Si en el universo siempre hay gravedad, dado que hay muchas masas y la fuerza gravitatoria tiene un radio de acción infinito, entonces todas las trayectorias en el espacio-tiempo han de ser líneas curvas. "¡Qué Universo tan curioso!", pensaría Einstein, "no hay trayectorias rectas, todos los cuerpos van en trayectorias curvas viajando por el espacio y por el tiempo... Entonces, ¿por qué empeñarse en describir el Universo usando un espacio plano de tres dimensiones... ¿No sería mucho mejor imaginar que el espacio-tiempo no es plano, sino que se ha "deformado" por las masas adquiriendo una geometría no-euclidiana?"
En el experimento 3 y el experimento 4 visualizaremos estos conceptos y aprenderemos otra cosa igual de extraña: en las geometrías no-euclidianas, las trayectorias que siguen los objetos sí son "rectas", pero en el sentido matemático más general de la palabra (es decir, las líneas más cortas entre dos puntos en esa geometría).
Resumiendo: desde el punto de vista de Newton, la Tierra sigue una trayectoria en el espacio euclidiano en forma de elipse (por cierto, es casi una circunferencia) alrededor del Sol. Desde el punto de vista de Einstein, la Tierra sigue la trayectoria más corta posible (una geodésica o "recta" generalizada) en un espacio-tiempo que ya no es euclidiano porque ha sido deformado por la masa del Sol.